Ratios
Unit Objective
●
Understand the concept of ratios and equivalent ratios
Key
Vocabulary
ratio

If there were two apples for every 1 orange,
the ratio of apples to oranges would
be 2:1.
equivalent

The twins were happy as long as they got an equivalent number of presents. When one
got more than the other, they were upset.
part-to-part ratio

"The ratio of apples to oranges is three
to five" is an example of a partto-part ratio because it compares two distinct parts of
a whole.
part-to-whole ratio

"The ratio of apples in the basket to
total fruits in the basket is three to eight" is an example of a part-to-whole ratio because it gives the
relationship between a part and the whole group.
Introduction
A ratio
is a comparison of two quantities. Consider two quantities a and b. The ratio a : b
indicates that there are units of the first quantity for every b units of the second quantity.
Ratios may also be written as fractions: 4 to 5 can be ⅘
You often use ratios. Look at these examples:
·
Scores in games are ratios. For example, the Penguins won 4 to 3,
or the Canucks lost 3 to 4.
·
The scale at the bottom of the maps is a ratio. For example, 1 centimeter
represents 10 kilometers.
·
Prices are often given as ratios. For example, 2 pounds for $3.79
or 2 cans for $1.85.
Phrases that indicate ratios are:
·
Let's
Practice
Using Ratios in a
Recipe
The ratio of iced tea to lemonade in a recipe
is 3 : 1. You begin by combining 3 cups of iced tea with 1 cup lemonade.

Use the following graph to answer the following
questions.
1.) Add 1 cup of iced tea and 1 cup of lemonade
to the mixture.
Does this change the taste of the mixture?
2.) Describe how you can make larger amounts
without changing the taste.

Writing
Ratios
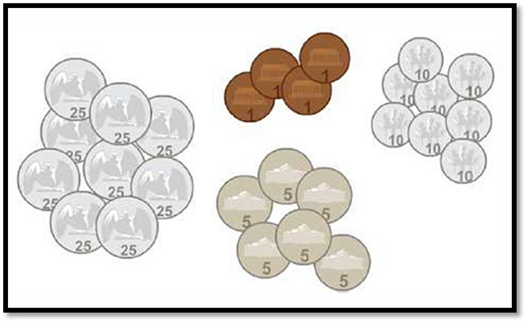
Look at the example of coins shown below:
|
|
To write the ratio of
pennies to quarters, you need to count the total number of pennies and
quarters.
So, the ratio of pennies
to quarters would be written as: 6 to 7 or 6 : 7 ------------------------------------------ To write the ratio of
quarters to dimes, you need to count the total number of quarters and dimes.
So, the ratio of
quarters to dimes would be written as: 7 to 3 or 7 : 3 |
Let's
Practice
Write the indicated
ratio using the coins in the example above.
1) dimes to pennies

2) quarters to pennies

3) quarters to the total number of coins

Writing Ratios from
Word Problems
Equivalent Ratios
A ratio can be represented as a fraction. The
concept of an equivalent ratio is similar to the concept of equivalent
fractions. A ratio that we get either by multiplying
or dividing by the same number, other
than zero, to the antecedent and the consequent of a ratio is called an equivalent ratio.
To get a ratio equivalent to a given ratio, you
first represent the ratio in fraction form. Then, we can get the equivalent
fraction by multiplying or dividing the first term and the second term by the
same non-zero number. At last, we represent it in the ratio form.
Look at the example below.
|
1 : 3 and 2 : 6 are equivalent
|
In Algebra, two ratios, a : b and c : d,
are equivalent when there exists a positive number n such that:
a
x n = c and b x n
= d.
Look at the example below and follow the
following steps.
I have 4 pennies, 6 nickels, 8 dimes, and 9 quarters
in my pocket.
What is the ratio of dimes to nickels?
Step 1: First, identify the
terms of the ratio.

Step 2: Write the ratio as a
fraction.

Step 3: Reduce the fraction,
if possible.

Answer: The ratio in its
lowest terms of dimes to nickels is 4/3
.

Let's Practice
Determining Whether
Ratios Are Equivalent
1. ) 4 : 3 and 20 : 15
You
can multiply each number in the first ratio by 5 to obtain the numbers in the
second ratio.
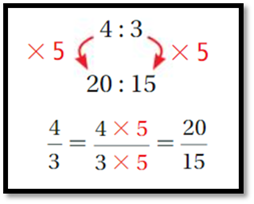
So, the ratio is ___________.

2. ) 5 : 7 and 10 : 21
You need to multiply each number in the ratio
by different amounts to obtain the numbers in the second ratio.
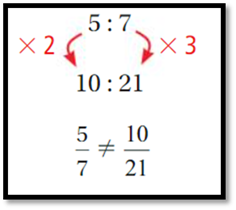
So,
the ratio is ______________.

Fill in the missing
number to complete each equivalent ratio.



